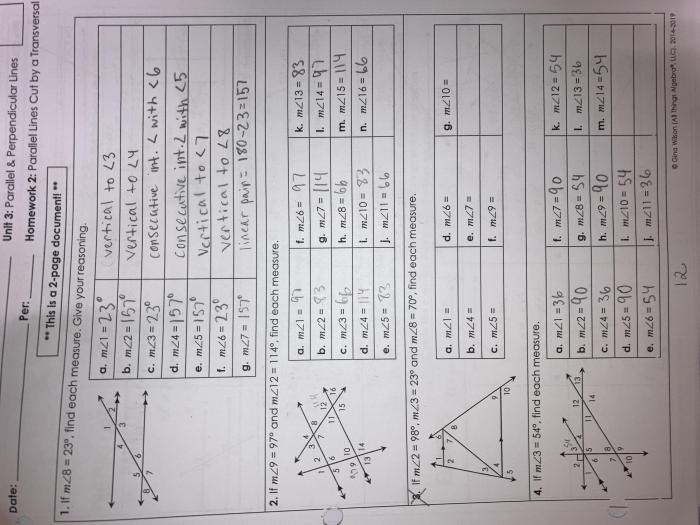
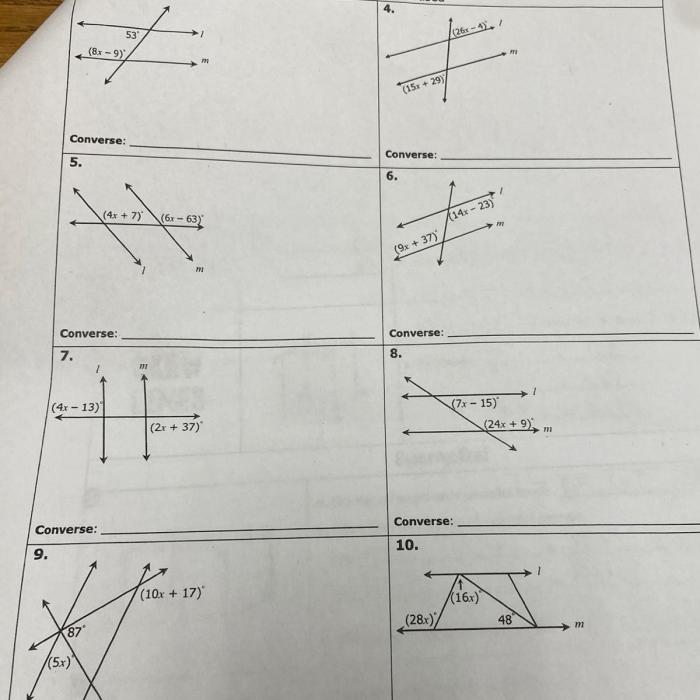
Delving into the realm of geometry, we present the Unit 3 Parallel and Perpendicular Lines Homework 4 Answer Key. This comprehensive guide unravels the intricacies of parallel and perpendicular lines, equipping you with the knowledge to conquer any geometry challenge.
Through lucid explanations, illustrative examples, and practical applications, this answer key empowers you to grasp the fundamental concepts of parallel and perpendicular lines, their properties, and their significance in the world around us.
Parallel and Perpendicular Lines: Unit 3 Parallel And Perpendicular Lines Homework 4 Answer Key

Lines are fundamental geometric entities that play a crucial role in various mathematical applications. Parallel and perpendicular lines are two important types of lines that exhibit distinct properties and have numerous real-world applications.
1. Parallel and Perpendicular Lines Definitions
Parallel linesare lines that never intersect and maintain a constant distance from each other. In other words, they are lines that lie in the same plane and do not diverge or converge.
Perpendicular lines, on the other hand, are lines that intersect at a right angle, forming a 90-degree angle at the point of intersection.
Visual examples of parallel and perpendicular lines can be seen in everyday objects such as railway tracks, window frames, and building structures.
2. Properties of Parallel and Perpendicular Lines
Parallel linesexhibit the following properties:
- They are equidistant from each other at all points.
- They never intersect, regardless of how far they are extended.
Perpendicular linespossess the following properties:
- They intersect at a right angle (90 degrees).
- The slopes of perpendicular lines are negative reciprocals of each other.
Both parallel and perpendicular lines find applications in various fields, including geometry, engineering, architecture, and design.
3. Identifying Parallel and Perpendicular Lines, Unit 3 parallel and perpendicular lines homework 4 answer key
Parallel linescan be identified using the following methods:
- Slope:Parallel lines have the same slope.
- Angle measurement:If two lines form an angle of 0 degrees, they are parallel.
Perpendicular linescan be identified using the following methods:
- Slope:Perpendicular lines have slopes that are negative reciprocals of each other.
- Angle measurement:If two lines form an angle of 90 degrees, they are perpendicular.
| Method | Parallel Lines | Perpendicular Lines |
|---|---|---|
| Slope | Same slope | Negative reciprocals |
| Angle measurement | 0 degrees | 90 degrees |
4. Applications of Parallel and Perpendicular Lines
Parallel lineshave numerous applications in geometry, such as:
- Constructing parallelograms
- Proving theorems about angles and triangles
Perpendicular linesalso have various applications in geometry, including:
- Constructing perpendicular bisectors
- Proving perpendicularity of lines
In addition to geometry, parallel and perpendicular lines have practical applications in engineering, architecture, and design. For example, in engineering, parallel lines are used to ensure the stability of bridges and other structures. In architecture, perpendicular lines are used to create right angles in buildings and other structures.
Detailed FAQs
What is the definition of parallel lines?
Parallel lines are two lines that never intersect, no matter how far they are extended.
How can I identify perpendicular lines?
Perpendicular lines intersect at a right angle (90 degrees).
What are some real-world applications of parallel and perpendicular lines?
Parallel lines are used in architecture to create buildings that are stable and aesthetically pleasing. Perpendicular lines are used in engineering to ensure that structures are strong and durable.