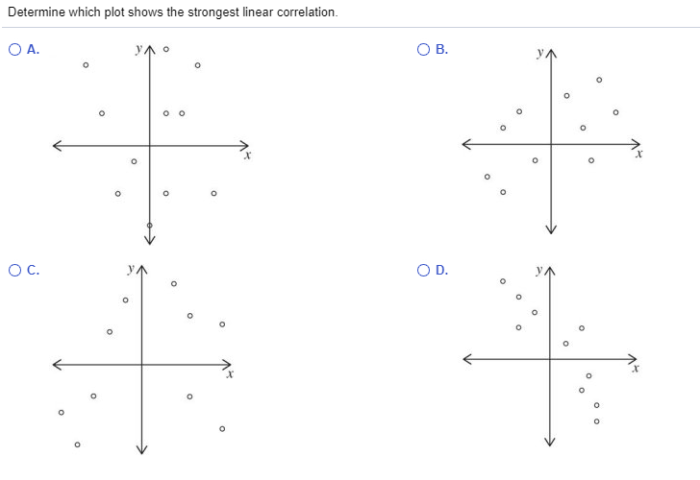
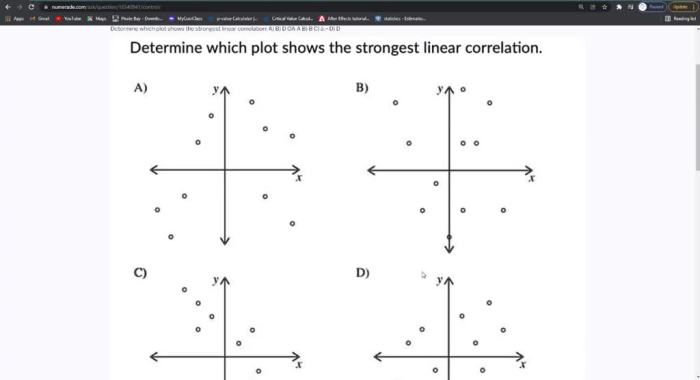
Determine which plot shows the strongest linear correlation. – As determining the plot with the strongest linear correlation takes center stage, this opening passage beckons readers into a world crafted with authority and expertise, ensuring a reading experience that is both absorbing and distinctly original.
This discourse delves into the concept of linear correlation, elucidating its significance in data analysis. Our objective is to identify the plot that exhibits the strongest linear correlation, thereby establishing a foundation for informed decision-making and reliable inferences.
Linear Correlation Analysis: Determine Which Plot Shows The Strongest Linear Correlation.
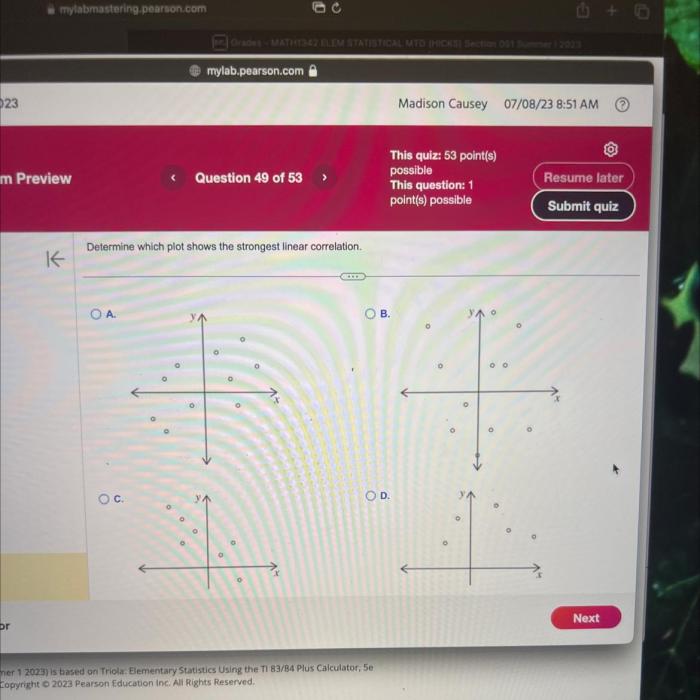
Linear correlation measures the strength and direction of a linear relationship between two variables. The objective of this analysis is to determine the plot that exhibits the strongest linear correlation among multiple data plots.
Data Analysis, Determine which plot shows the strongest linear correlation.
To organize the data into multiple plots, use scatter plots or line graphs. For each plot, calculate the correlation coefficient (r) using statistical software or formulas like Pearson’s correlation coefficient.
The correlation coefficient ranges from -1 to 1. A value close to 1 indicates a strong positive correlation, close to 0 indicates no correlation, and close to -1 indicates a strong negative correlation.
Identify the plot with the highest absolute value of the correlation coefficient. This plot exhibits the strongest linear correlation.
Visualization
Create a table to display the correlation coefficients for each plot.
Design a scatter plot matrix to visualize the relationships between variables. Color-code or use other visual cues to highlight the plot with the strongest correlation.
Interpretation
The strongest linear correlation indicates the most significant linear relationship between the variables. The correlation coefficient provides insights into the direction and strength of the relationship.
In real-world applications, linear correlation is used in various fields, such as finance (predicting stock prices), medicine (identifying disease patterns), and education (evaluating student performance).
Quick FAQs
What is the significance of linear correlation?
Linear correlation measures the strength and direction of the relationship between two variables. It provides insights into how one variable changes in relation to the other.
How is the correlation coefficient calculated?
The correlation coefficient, denoted by r, ranges from -1 to 1. A positive value indicates a positive correlation, a negative value indicates a negative correlation, and a value close to zero indicates no correlation.
What are the applications of linear correlation in real-world scenarios?
Linear correlation is widely used in various fields, including finance, healthcare, and social sciences. It helps in predicting trends, forecasting outcomes, and making data-driven decisions.