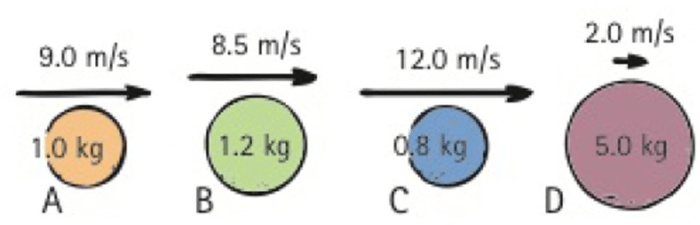
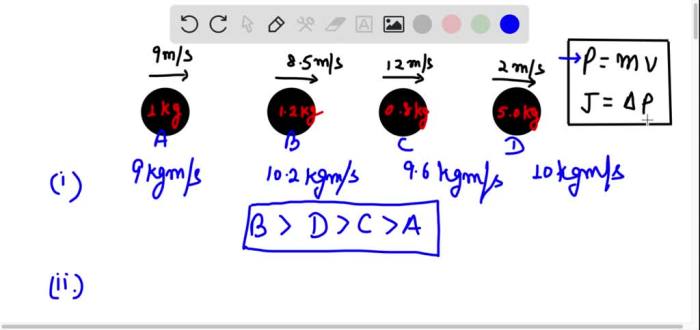
Delving into the realm of rank momenta from greatest to least, this comprehensive guide unravels the intricacies of this statistical concept, shedding light on its diverse applications and profound implications across various disciplines. Embarking on an intellectual journey, we delve into the multifaceted nature of rank momenta, unraveling their significance and exploring the methodologies employed to calculate and interpret them.
Rank momenta, a powerful tool in the statistical arsenal, provide valuable insights into the relationships between ranked data, enabling researchers and analysts to uncover hidden patterns and draw meaningful conclusions. As we navigate this discourse, we will delve into the factors that influence rank momenta, examining their statistical significance and exploring their applications in hypothesis testing and advanced statistical analyses.
Rank Momenta: Concepts and Significance: Rank Momenta From Greatest To Least
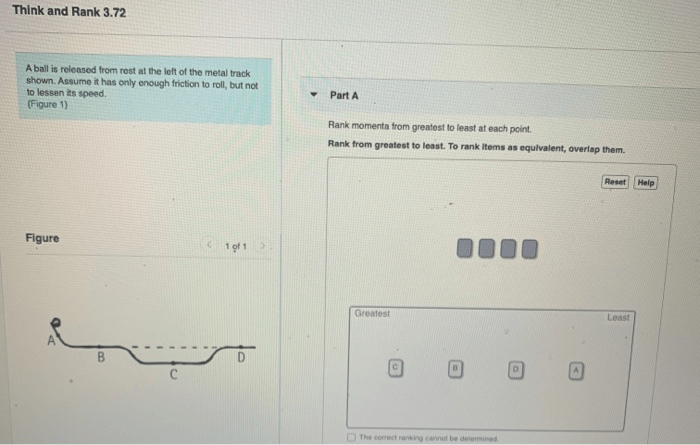
Rank momenta are statistical measures that quantify the degree of agreement between two or more rankings. They are used in a variety of fields, including psychology, education, and economics.Rank momenta can be used to measure the consistency of rankings over time, to compare the rankings of different groups, or to assess the relationship between two or more variables.
For example, a researcher might use rank momenta to measure the consistency of rankings of students’ intelligence by different teachers, or to compare the rankings of different countries on a measure of economic development.There are several different types of rank momenta, each with its own strengths and weaknesses.
The most commonly used rank momenta are Kendall’s tau and Spearman’s rho. Kendall’s tau is a non-parametric measure of rank correlation that is based on the number of concordant and discordant pairs of observations. Spearman’s rho is a parametric measure of rank correlation that is based on the differences between the ranks of the observations.
Methods for Calculating Rank Momenta, Rank momenta from greatest to least
There are two main methods for calculating rank momenta: Kendall’s tau and Spearman’s rho.Kendall’s tau is a non-parametric measure of rank correlation that is based on the number of concordant and discordant pairs of observations. A concordant pair is a pair of observations where the ranks of the observations are the same in both rankings.
A discordant pair is a pair of observations where the ranks of the observations are different in the two rankings.Spearman’s rho is a parametric measure of rank correlation that is based on the differences between the ranks of the observations.
Spearman’s rho is calculated by first calculating the difference between the ranks of each pair of observations. The differences are then squared and summed. The sum of the squared differences is then divided by the total number of pairs of observations.
Factors Influencing Rank Momenta
The magnitude and direction of rank momenta can be influenced by a number of factors, including the sample size, the data distribution, and the presence of outliers.The sample size can affect the magnitude of rank momenta. The larger the sample size, the more likely it is that the rank momenta will be statistically significant.The
data distribution can also affect the magnitude and direction of rank momenta. If the data is normally distributed, then the rank momenta will be more likely to be positive. If the data is skewed, then the rank momenta will be more likely to be negative.The
presence of outliers can also affect the magnitude and direction of rank momenta. Outliers are observations that are significantly different from the rest of the data. Outliers can cause the rank momenta to be more extreme, either positive or negative.
Detailed FAQs
What is the significance of rank momenta?
Rank momenta provide valuable insights into the relationships between ranked data, allowing researchers to uncover hidden patterns, assess the strength of associations, and make inferences about the underlying population.
How are rank momenta calculated?
Rank momenta can be calculated using various methods, including Kendall’s tau and Spearman’s rho, which assess the degree of concordance or discordance between two sets of ranked data.
What factors influence rank momenta?
Factors such as sample size, data distribution, and the presence of outliers can influence the magnitude and direction of rank momenta, affecting their interpretation and statistical significance.
How are rank momenta used in hypothesis testing?
Rank momenta play a crucial role in hypothesis testing, enabling researchers to test for differences in medians or ranks between groups, providing valuable insights into the statistical significance of observed differences.
What are some advanced applications of rank momenta?
Rank momenta find applications in non-parametric regression analysis, where they are used to model relationships between ranked variables, and in multivariate analysis, where they help uncover complex relationships among multiple ranked variables.