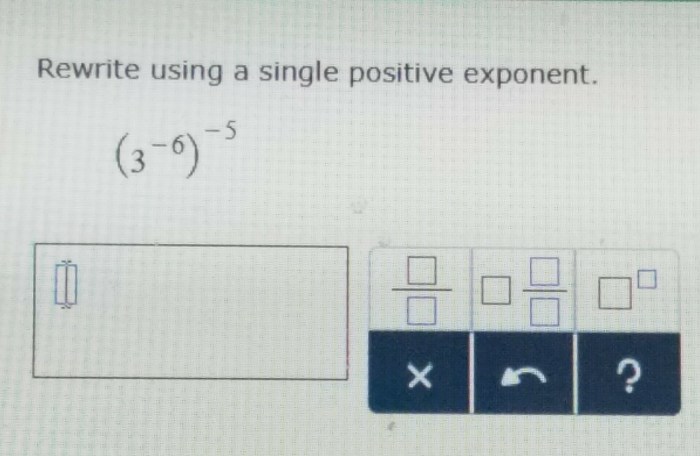
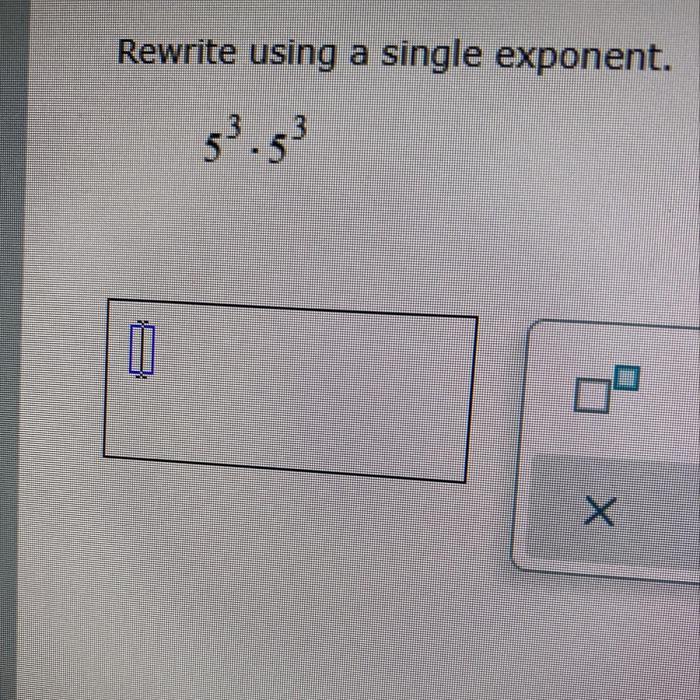
Rewrite using a single exponent. – Rewrite using a single exponent is a powerful technique that allows us to simplify complex expressions and make them more manageable. This process involves expressing multiple exponents as a single, combined exponent, providing numerous benefits in various mathematical applications.
By understanding the methods and benefits of rewriting using a single exponent, we can enhance our mathematical skills and gain a deeper understanding of algebraic concepts.
Understanding Rewrite Using a Single Exponent
Rewriting an expression using a single exponent involves expressing a complex expression with multiple exponents as a single, simplified exponent. This process simplifies calculations and makes expressions more manageable.
To rewrite using a single exponent, follow these steps:
- Identify the base and the exponents of each term.
- Multiply the exponents of terms with the same base.
- Combine the bases by multiplying them.
For example, (x 2y 3) 4can be rewritten as x 8y 12.
Methods for Rewriting Using a Single Exponent
Using Laws of Exponents:
Apply laws of exponents, such as (a m) n= a mn, to combine exponents with the same base.
Factoring:
Factor out common terms to identify terms with the same base and exponents.
Example:
(x 2+ 2x)(x 2– 2x) = (x 2)(x 2) – (2x)(x 2) + (2x)(x) – (2x)(2x) = x 4– 2x 3+ 2x 2– 4x
Benefits of Rewriting Using a Single Exponent
Simplifies Calculations:
Combining exponents simplifies calculations by reducing the number of operations.
Makes Expressions More Manageable:
Rewriting expressions with a single exponent makes them easier to read, write, and understand.
Example:
Rewriting (2 3)(2 4)(2 5) as 2 12simplifies calculations and makes the expression more manageable.
Examples and Applications, Rewrite using a single exponent.
Example 1:
Rewrite (x 2y 3) 4using a single exponent.
Solution:
x 8y 12
Application:
In algebra, rewriting expressions using a single exponent simplifies polynomial multiplication.
Example 2:
Rewrite (2 3+ 3 2)(2 3– 3 2) using a single exponent.
Solution:
8 – 9 = -1
Application:
In calculus, rewriting expressions using a single exponent simplifies differentiation and integration.
Design a Table Illustrating Rewrite Rules
| Original Expression | Steps | Rewritten Expression |
|---|---|---|
| (x2y3)4 | (x2)4(y3)4 = x8y12 | x8y12 |
(x + 2)(x
|
(x2
|
x2
|
Visual Aids and Illustrations
Flowchart:
Start:Expression with multiple exponents
Step 1:Identify base and exponents
Step 2:Apply laws of exponents or factoring
Step 3:Combine bases and exponents
End:Expression with a single exponent
FAQ Corner: Rewrite Using A Single Exponent.
What is the main purpose of rewriting using a single exponent?
The primary purpose is to simplify complex expressions, making them more manageable and easier to work with.
What are the benefits of rewriting using a single exponent?
Benefits include simplified calculations, enhanced understanding, and wider applicability in various mathematical fields.
What are some common methods used for rewriting using a single exponent?
Common methods include using the laws of exponents, factoring, and combining like terms.